Die Hauptgebiete 1. Experimentalphysik 1-4 35. Schrödinger-Gleichung  | 8. Der harmonische Oszillator: |
 | Schrödingergleichung des harmonischen Oszillators: |
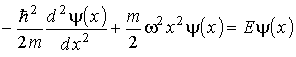
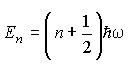| Energieeigenwerte des harmonischen Oszillators: n heißt Quantenzahl |
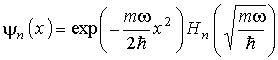
| Zugehörige Eigenfunktionen: mit Hn = Hermitesche Polynome |
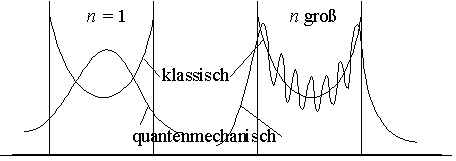
| Aufenthaltswahrscheinlichkeit: Korrespondenzprinzip: Für große n nähert sich die quantenmechanische Lösung der klassischen an |
| Nullpunktsenergie (für n = 0) :  |
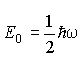
| Querverweise: Schulphysik: Beispiele für mechanische harmonische Schwingungen |
| 14.09.2000 - URL dieser Seite - Seite_ID: 1035008 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |
 | 9. Hohlraumstrahlung |
 | KI Antworten zu diesem Thema: (kostenlos und ohne Anmeldung) |
|
powered by askfree.ai
|
 | Literatur zu diesem Thema: |
Unser Partner amazon.de liefert ab 20 Euro  - mehr Bücher im Buchshop |
 | Diskussionsbeiträge zu dieser Seite: |
|
aus dem Physik-Forum:
|
|
| |
35. Schrödinger-Gleichung | 1. Klassische Physik - Quantenmechanik |
| 2. Zeitabhängige Schrödingergleichung |
| 3. Eigenschaften der Lösung der Schrödingergleichung |
| 4. Zeitunabhängige Schrödingergleichung |
| 5. Teilchen im Kastenpotential |
| 6. Potentialstufe |
| 7. Potentialbarriere und Tunneleffekt |
| 8. Der harmonische Oszillator |
| 9. Hohlraumstrahlung |