
 | 
3. Vertauschungsrelationen mit dem Drehimpulsoperator:
|
|
|
 | [Lx, x] = 0; [Lx, y] = i 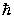 z; [Lx, z] = -i z; [Lx, z] = -i 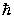 y y
|
|
|
 | [Lx, px] = 0; [Lx, py] = i 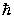 pz; [Lx, pz] = -i pz; [Lx, pz] = -i 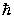 py py
|
|
|
 | [Lx, x2] = 0; [Lx, y2] = 2i 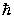 yz; [Lx, z2] = -2i yz; [Lx, z2] = -2i 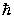 yz yz
|
|
|
 | [Lx/y/z, x2 + y2 + z2 ] = 0; => [ 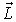 , r2] = 0 , r2] = 0
|
|
|
 | [ 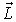 , F(r)] = 0 allgemein , F(r)] = 0 allgemein
|
|
|
 | [Lx, px2] = 0; [Lx, py2] = 2i 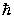 py pz; [Lx, pz2] = -2i py pz; [Lx, pz2] = -2i 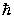 py pz py pz
|
|
|
 | [ 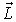 , p2] = 0; allgemein: [ , p2] = 0; allgemein: [ 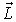 , F(p)] = 0 , F(p)] = 0
|
|
|
 | => [Lx, H] = 0; [Ly, H] = 0; [Lz, H] = 0; [ 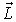 , H] = 0 , H] = 0
nur bei zentralsymmetrischem Potential
|
|
|
 | [Lx, Ly] = i 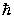 Lz; [Ly, Lz] = i Lz; [Ly, Lz] = i 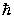 Lx; [Lz, Lx] = i Lx; [Lz, Lx] = i 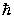 Ly Ly
|
|
|
 | [ 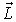 2, Lx] = 0; [ 2, Lx] = 0; [ 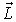 2, Ly] = 0; [ 2, Ly] = 0; [ 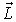 2, Lz] = 0 2, Lz] = 0
|
|
|
 | Aus [ 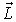 , H] = 0 im rotationssymmetrischen Potential folgt , H] = 0 im rotationssymmetrischen Potential folgt
[ 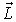 2, H] = 0 2, H] = 0
|
|
|
 | Querverweise:
Quantenmechanik: Drehimpulsoperator Drehimpulsoperator in sphärischen Koordinaten
|
|
|
 | 08.01.2001 - URL dieser Seite - Seite_ID: 5010003
Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |














 - mehr Bücher im
- mehr Bücher im