
7. Kugelfunktionen:

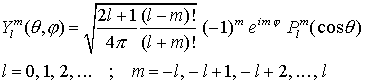

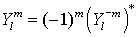

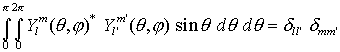



Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema
 | 7. Kugelfunktionen: |
 | Definition: 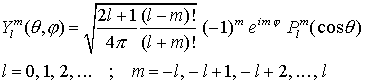 |
 | 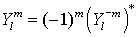 |
 | Die Kugelfunktionen sind orthonormal auf der Einheitskugel 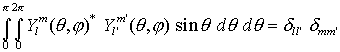 |
 | Die Kugelfunktionen bilden einen vollständigen Satz, d.h. jede Funktion auf der Einheitskugel kann nach den Kugelfunktionen entwickelt werden |
 | Die ersten drei Kugelfunktionen:  |
| 22.01.2001 - URL dieser Seite - Seite_ID: 5011007 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |
 | 8. Gemeinsame Eingenfunktionen der z-Komponente und des Quadrates des Drehimpulsoperators |
| Literatur zu diesem Thema: | |
Unser Partner amazon.de liefert ab 20 Euro  - mehr Bücher im Buchshop - mehr Bücher im Buchshop |
| Diskussionsbeiträge zu dieser Seite: (Neuer Beitrag) | |
 |
aus dem Physik-Forum:
|
|
| |
| 1. Differentialbeziehungen in sphärischen Koordinaten |
| 2. Drehimpulsoperator in sphärischen Koordinaten |
| 3. Zeitunabhängige Schrödinger-Gleichung in sphärischen Koordinaten |
| 4. Radiale Schrödinger-Gleichung |
| 5. Legendre Polynome |
| 6. Assozierte Legendre Funktionen |
| 7. Kugelfunktionen |
| 8. Gemeinsame Eingenfunktionen der z-Komponente und des Quadrates des Drehimpulsoperators |
| 9. Normierung in sphärisch symmetrischen Potentialen |
| 10. Wahrscheinlichkeitsdichte - in kartesichen Koordinaten - in Kugelkoordinaten |
| 11. Leiteroperatoren |