
6. Partialwellenzerlegung:

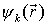 können nach radialen Eigenfunktionen des Potentials und Kugelfunktionen entwickelt werden:
können nach radialen Eigenfunktionen des Potentials und Kugelfunktionen entwickelt werden: 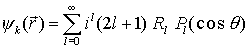
(wegen Unabhängigkeit von
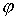 tritt nur
tritt nur 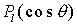 auf)
auf) 
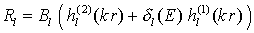 ;
; 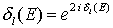 elastische Streuung
elastische Streuung 
 bestehen aus der einfallenden ebenen Welle und der Kugelwelle mit Streuamplitude. Die ebene Welle kann nach Kugelwellen entwickelt werden.
bestehen aus der einfallenden ebenen Welle und der Kugelwelle mit Streuamplitude. Die ebene Welle kann nach Kugelwellen entwickelt werden. Die Streuamplitude kann nach Kugelfunktionen entwickelt werden
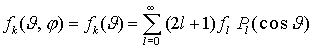
die Entwicklungskoeffizienten fl heißen Partialwellenamplituden

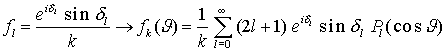
(gilt nur für elastische Streuung)

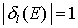 . Die Amplitude der auslaufenden Kugelwelle ist gegenüber der einlaufenden unverändert, aber die Phase ändert sich
. Die Amplitude der auslaufenden Kugelwelle ist gegenüber der einlaufenden unverändert, aber die Phase ändert sich Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

 - mehr Bücher im
- mehr Bücher im