
 | 
11. Fermis Goldene Regel:
|
|
|
 | Man erhält die goldene Regel auch durch Berechnung der zeitlichen Entwicklung eines gestörten Systems bei zeitunabhängiger Störung durch 1. Ordnung Störungsrechnung
|
|
|
 | Die Übergangswahrscheinlichkeit von einem Zustand  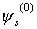 des ungestörten Hamilton in ein Intervall des ungestörten Hamilton in ein Intervall  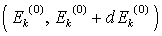 ist dann: ist dann:
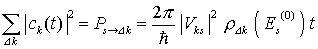
 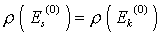 Niveaudichte Niveaudichte
(gilt nur unter den unten gegebenen Bedingungen)
|
|
|
 | Die goldene Regel (Übergangsrate = Übergangswahrscheinlichkeit pro Zeiteinheit) ist dann:
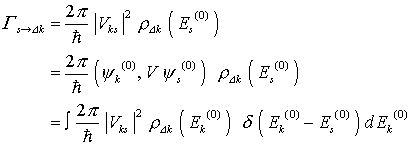
wegen Energieerhaltung  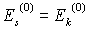
|
|
|
 | Die goldene Regel gilt auch für Übergänge aus einem Kontinuum von Anfangszuständen  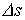 in einen diskreten Endzustand k, in diesem Fall muß über die Anfangszustände summiert werden: in einen diskreten Endzustand k, in diesem Fall muß über die Anfangszustände summiert werden:
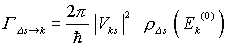
|
|
|
 | Die goldene Regel gilt nur, wenn Anfangs- oder Endzustand ein Intervall mit quasikontinuierlichem Spektrum ist, und das Intervall größer als die Breite der  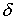 artigen Funktion ist artigen Funktion ist
|
|
|
 | Querverweise:
Quantenmechanik: Fermis Goldene Regel bei zeitabhängiger Störung
|
|
|
 | 07.03.2001 - URL dieser Seite - Seite_ID: 5015011
Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |



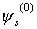 des ungestörten Hamilton in ein Intervall
des ungestörten Hamilton in ein Intervall 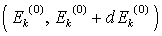 ist dann:
ist dann: 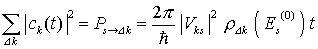
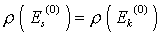 Niveaudichte
Niveaudichte 
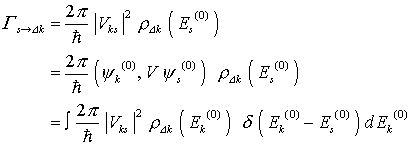
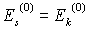

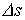 in einen diskreten Endzustand k, in diesem Fall muß über die Anfangszustände summiert werden:
in einen diskreten Endzustand k, in diesem Fall muß über die Anfangszustände summiert werden: 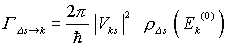

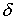 artigen Funktion ist
artigen Funktion ist 


 - mehr Bücher im
- mehr Bücher im