
13. Paschen-Back-Effekt:

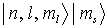
mit
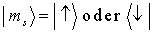 berechnet
berechnet 
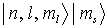 sind Eigenzustände von H0 L2 Lz S2 Sz und diagonalisieren Hz (Durch das starke Feld wird die Spin-Bahn-Kopplung aufgehoben)
sind Eigenzustände von H0 L2 Lz S2 Sz und diagonalisieren Hz (Durch das starke Feld wird die Spin-Bahn-Kopplung aufgehoben) 
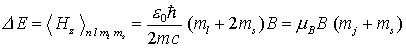

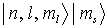 berechnet werden
berechnet werden 
| ml | ms | ml+2ms | ||
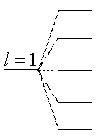 | 1 0 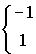 0 1 | 1/2 1/2 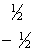 -1/2 -1/2 | 3/2 1/2 -1/2 3/2 | (Haken Wolf) (l = 1 wegen relativistischer Massenkorrektur abgesenkt) |
Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema


 - mehr Bücher im
- mehr Bücher im