Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

20. Moleküle

	1. Born-Oppenheimer-Näherung:
	Die Born-Oppenheimer-Gleichung ist die Schrödinger-Gleichung für die Kerne in Molekülen
	Hamilton Operator des Moleküls:  H = Te + TK + Vee + VeK + VKK
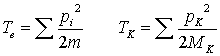
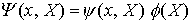
	Ansatz für die Gesamtwellenfunktion x = Elektronenkoordinaten X = Kernkoordinaten
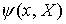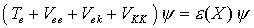
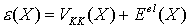
	Bei festen Kernen erfüllt  die Schrödinger-Gleichung mit  Die Kernlagen X sind Parameter
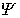	Durch Einsetzen des Ansatzes  in die gesamte Schrödinger-Gleichung 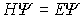mit Benutzung der Schrödinger-Gleichung für  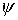und Vernachlässigung von Termen (Born-Oppenheimer-Näherung) folgt die Born-Oppenheimer-Gleichung: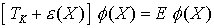 Aus 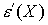= 0  folgt die Gleichgewichtslage der Kerne
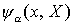	Durch Berücksichtigung von verschiedenen elektronischen Zuständen folgt mit Entwicklung von 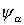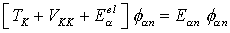nach den : (Born-Oppenheimer-Gleichung)
	Die Kerne bewegen sich im effektiven Potential der Kernabstoßung und elektronischen Energie
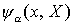	Bei bekannten Elektronen-Wellenfunktionen mit festen Kernen und elektronischen Energien  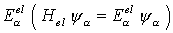lässt sich aus der Born-Oppenheimer-Gleichung die Gesamtwellenfunktion  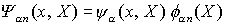bestimmen
	Querverweise: Quantenmechanik:   Bornsche Näherung in der Streutheorie   Beispiel: Bornsche Näherung im rotationssymmetrischen Potential
	12.06.2001 - URL dieser Seite - Seite_ID: 5020001 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

2. Das Wasserstoffmolekül mit nur einem Elektron

	Literatur zu diesem Thema:
	Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop

sponsored Link: Meta-Preisvergleich


Kapitelübersicht
20. Moleküle

1. Born-Oppenheimer-Näherung

2. Das Wasserstoffmolekül mit nur einem Elektron

3. Das Wasserstoffmolekül (Wellenfunktionen der Elektronen bei festen Kernen)

4. Energie des Wasserstoffmoleküls

5. Kernwellenfuktion beim zweiatomigen Molekül

6. Van der Waals Kraft