
1. Schrödingergleichung des Wasserstoff-Atoms:

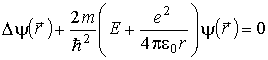
m kann durch

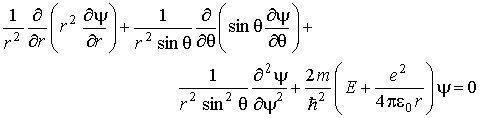

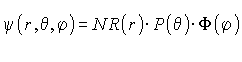
(1)
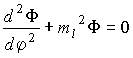
(2)
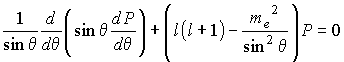
(3)
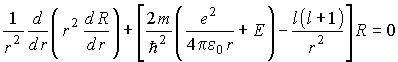
Lösung:
R enthalten Laguerre Polynome, Y = N P = Kugelflächenfunktionen, P = assoziierte Legendre Polynome

l = 0...(n-1) Nebenquantenzahl
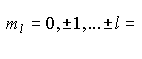 magnetische Quantenzahl
magnetische Quantenzahl

Experimentalphysik 1-4: Zeitabhängige Schrödingergleichung Eigenschaften der Lösung der Schrödingergleichung Zeitunabhängige Schrödingergleichung
Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema


 - mehr Bücher im
- mehr Bücher im