Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

6. Harmonischer Oszillator

	4. Hermitesche Polynome:
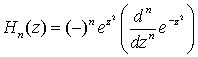	Definition:   ; n = 0, 1, 2, ... Hn ist ein Polynom vom Grade n und der Parität (-)n und besitzt n Nullstellen
	Erzeugende Funktion:
	Rekursionsformel:
	Die ersten 3 Hermite Polynome:
	Rekursionsformel:
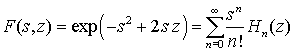
	Querverweise: Quantenmechanik:   Legendre Polynome   Laguerre Polynome
	09.08.2000 - URL dieser Seite - Seite_ID: 5006004 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

5. Eigenfunktionen des harmonischen Oszillators

	Literatur zu diesem Thema:
	Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop

sponsored Link: Meta-Preisvergleich


Kapitelübersicht
6. Harmonischer Oszillator

1. Schrödinger-Gleichung des harmonischen Oszillators

2. Lösung der Schrödinger-Gleichung des harmonischen Oszillators

3. Energieeigenwerte des harmonischen Oszillators

4. Hermitesche Polynome

5. Eigenfunktionen des harmonischen Oszillators

6. Vergleich der klassischen und quantenmechanischen Behandlung des harmonischen Oszillators

7. Algebraische Methode zur Bestimmung der Wellenfunktion des harmonischen Oszillators (mit Auf- und Absteigeoperatoren)

8. Zustandssumme des harmonischen Oszillators