Die Hauptgebiete 5. Quantenmechanik 11. Sphärisch symmetrische Potentiale  | 5. Legendre Polynome: |
 | Definition:   |
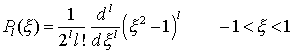
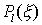| Grad von  : l Parität: (-1) l Orthonormierung:   |
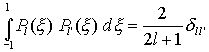
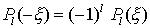
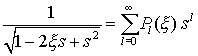
| Erzeugende Funktion:  (Diese Funktion lässt sich in eine Potenzreihe mit den Koeffizienten 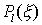entwickeln) |
| Die Legendre Polynome sind Lösungen der Differentialgleichung:  |
| Die ersten drei Legendre Polynome:  |
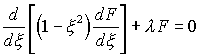
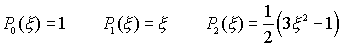
| Querverweise: Quantenmechanik: Hermitesche Polynome Assozierte Legendre Funktionen Laguerre Polynome |
| 15.01.2001 - URL dieser Seite - Seite_ID: 5011005 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |
 | 6. Assozierte Legendre Funktionen |
 | Literatur zu diesem Thema: |
Unser Partner amazon.de liefert ab 20 Euro  - mehr Bücher im Buchshop |
|
| |
11. Sphärisch symmetrische Potentiale | 1. Differentialbeziehungen in sphärischen Koordinaten |
| 2. Drehimpulsoperator in sphärischen Koordinaten |
| 3. Zeitunabhängige Schrödinger-Gleichung in sphärischen Koordinaten |
| 4. Radiale Schrödinger-Gleichung |
| 5. Legendre Polynome |
| 6. Assozierte Legendre Funktionen |
| 7. Kugelfunktionen |
| 8. Gemeinsame Eingenfunktionen der z-Komponente und des Quadrates des Drehimpulsoperators |
| 9. Normierung in sphärisch symmetrischen Potentialen |
| 10. Wahrscheinlichkeitsdichte - in kartesichen Koordinaten - in Kugelkoordinaten |
| 11. Leiteroperatoren |