Die Hauptgebiete 5. Quantenmechanik 11. Sphärisch symmetrische Potentiale  | 6. Assozierte Legendre Funktionen: |
 | Definition:    |
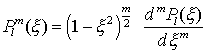
| Eigenschaften: für m > l ist    |
| Orthonormierung:  |
| Die assoziierten Legendre Funktionen sind Lösungen der Differentialgleichung:  |
| Die ersten drei Funktionen sind:  |
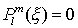
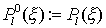
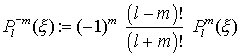
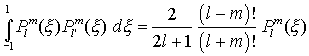
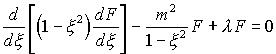
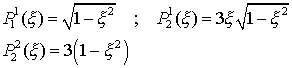
| Querverweise: Experimentalphysik 1-4: Fourier-Analyse für periodische Funktionen Fourier-Analyse für nicht periodische Funktionen Quantenmechanik: Entwicklung von Funktionen Skalarprodukt von Funktionen Funktionen von Operatoren Legendre Polynome |
| 18.01.2001 - URL dieser Seite - Seite_ID: 5011006 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |
 | 7. Kugelfunktionen |
 | Literatur zu diesem Thema: |
Unser Partner amazon.de liefert ab 20 Euro  - mehr Bücher im Buchshop |
|
| |
11. Sphärisch symmetrische Potentiale | 1. Differentialbeziehungen in sphärischen Koordinaten |
| 2. Drehimpulsoperator in sphärischen Koordinaten |
| 3. Zeitunabhängige Schrödinger-Gleichung in sphärischen Koordinaten |
| 4. Radiale Schrödinger-Gleichung |
| 5. Legendre Polynome |
| 6. Assozierte Legendre Funktionen |
| 7. Kugelfunktionen |
| 8. Gemeinsame Eingenfunktionen der z-Komponente und des Quadrates des Drehimpulsoperators |
| 9. Normierung in sphärisch symmetrischen Potentialen |
| 10. Wahrscheinlichkeitsdichte - in kartesichen Koordinaten - in Kugelkoordinaten |
| 11. Leiteroperatoren |