Die Hauptgebiete 1. Experimentalphysik 1-4 26. Interferenz von Schwingungen und Wellen  | 8. Fourier-Analyse für periodische Funktionen: |
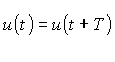 | Jede periodische Funktion läßt sich aus einer Grundschwingung der Frequenz und ihren Oberschwingungen aufbauen: mit 
|
| Komplexe Schreibweise: mit  |
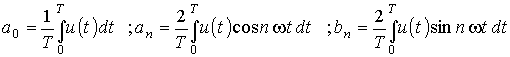
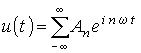
| Analog für örtlich periodische Funktionen  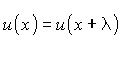mit 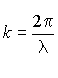 statt |
| Querverweise: Experimentalphysik 1-4: Fourier-Analyse für nicht periodische Funktionen Quantenmechanik: Entwicklung von Funktionen Skalarprodukt von Funktionen Funktionen von Operatoren Assozierte Legendre Funktionen |
| 12.09.2000 - URL dieser Seite - Seite_ID: 1026008 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |
 | 9. Fourier-Analyse für nicht periodische Funktionen |
 | Metasuche zu diesem Thema: |
| Mit der Metasuche finden sie weitere Informationen zu diesem Thema. Die Metasuche durchsucht ausgewählte Online-Quellen aus verschiedenen Bereichen. Das Suchergebnis enthält nach Möglichkeit Auszüge aus den besten Ergebnisseiten und direkte Links zu den Quellen: Texte (Vorlesungen, Artikel) Aufgaben (Prüfungen, Übungen) Simulationen (Java-Applets, Englisch) Referate, Hausaufgaben Versuche |
 | Literatur zu diesem Thema: |
Unser Partner amazon.de liefert ab 20 Euro  - mehr Bücher im Buchshop |
|
| |
26. Interferenz von Schwingungen und Wellen | 1. Überlagerung zweier Wellen gleicher Frequenz und Amplitude |
| 2. Überlagerung von Schwingungen verschiedener Frequenz |
| 3. Überlagerung von Wellen verschiedener Frequenz |
| 4. Gruppengeschwindigkeit |
| 5. Reflexion von Wellen |
| 6. Stehende Wellen |
| 7. Eigenschwingungen |
| 8. Fourier-Analyse für periodische Funktionen |
| 9. Fourier-Analyse für nicht periodische Funktionen |
| 10. Fourier-Analyse einer Welle |
| 11. Mehrdimensionale Wellen |
| 12. Doppler-Effekt |
| 13. Machscher Kegel |
| 14. Schwingungen und stehende Wellen in mehreren Dimensionen |