Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

11. Sphärisch symmetrische Potentiale



10. Wahrscheinlichkeitsdichte - in kartesichen Koordinaten - in Kugelkoordinaten:

In kartesischen Koordinaten wird die 
Aufenthaltswahrscheinlichkeit  
im Element  angegeben

Die Wahrscheinlichkeitsdichte ist 

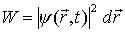
Transformation auf Kugelkoordinaten ergibt

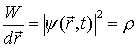
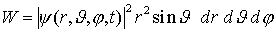
=> Wahrscheinlichkeitsdichte: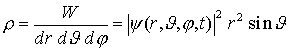

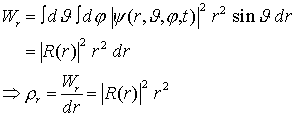
Die radiale Wahrscheinlichkeitsdichte ergibt sich durch Integration über die Winkel:


Querverweise:
Quantenmechanik:   Differentialbeziehungen in sphärischen Koordinaten   Drehimpulsoperator in sphärischen Koordinaten   Zeitunabhängige Schrödinger-Gleichung in sphärischen Koordinaten   Freies Teilchen in Kugelkoordinaten

24.01.2001 - URL dieser Seite - Seite_ID: 5011010
Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

11. Leiteroperatoren


Literatur zu diesem Thema:
 
 Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop



sponsored Link: Meta-Preisvergleich


Kapitelübersicht

11. Sphärisch symmetrische Potentiale

1. Differentialbeziehungen in sphärischen Koordinaten
2. Drehimpulsoperator in sphärischen Koordinaten
3. Zeitunabhängige Schrödinger-Gleichung in sphärischen Koordinaten
4. Radiale Schrödinger-Gleichung
5. Legendre Polynome
6. Assozierte Legendre Funktionen
7. Kugelfunktionen
8. Gemeinsame Eingenfunktionen der z-Komponente und des Quadrates des Drehimpulsoperators
9. Normierung in sphärisch symmetrischen Potentialen
10. Wahrscheinlichkeitsdichte - in kartesichen Koordinaten - in Kugelkoordinaten
11. Leiteroperatoren