Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

11. Sphärisch symmetrische Potentiale

	8. Gemeinsame Eingenfunktionen der z-Komponente und des Quadrates des Drehimpulsoperators:
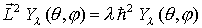	Herleitung: Lösung der Gleichung  durch den Seperationsansatz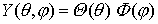
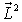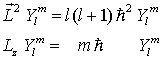
	Die Eigenfunktionen von  sind gleichzeitig Eigenfunktionen  von Lz: 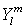sind die Kugelfunktionen
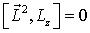	Das ist möglich weil     ( Vertauschungsrelationen mit dem Drehimpulsoperator )
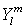	Die Funktionen   sind keine Eigenfunktionen von Lx und Ly , weil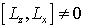
	Querverweise: Quantenmechanik:   Gemeinsame Eigenfunktionen der z-Komponente und des Quadrates des Gesamtdrehimpulses   Gemeinsame Eigenfunktionen der z-Komponente und des Quadrates des Gesamtdrehimpulses bei Addition von beliebigen Drehimpulsen
	23.01.2001 - URL dieser Seite - Seite_ID: 5011008 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

9. Normierung in sphärisch symmetrischen Potentialen

	Bildschirmexperimente zu diesem Thema:
	dim.modul Polarisationsfilter 1 [Beschreibung] [Download]
	Bildschirmexperimente und Beschreibungen: © dim.digitale medien  -  mehr Experimente...

	Literatur zu diesem Thema:
	Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop

sponsored Link: Meta-Preisvergleich


Kapitelübersicht
11. Sphärisch symmetrische Potentiale

1. Differentialbeziehungen in sphärischen Koordinaten

2. Drehimpulsoperator in sphärischen Koordinaten

3. Zeitunabhängige Schrödinger-Gleichung in sphärischen Koordinaten

4. Radiale Schrödinger-Gleichung

5. Legendre Polynome

6. Assozierte Legendre Funktionen

7. Kugelfunktionen

8. Gemeinsame Eingenfunktionen der z-Komponente und des Quadrates des Drehimpulsoperators

9. Normierung in sphärisch symmetrischen Potentialen

10. Wahrscheinlichkeitsdichte - in kartesichen Koordinaten - in Kugelkoordinaten

11. Leiteroperatoren