Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

20. Moleküle

	2. Das Wasserstoffmolekül mit nur einem Elektron:
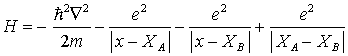
	Hamilton-Operator des Elektrons x = Koordinaten des Elektrons XA = Koordinaten von Kern A XB = Koordinaten von Kern B
	Das Problem ist exakt lösbar
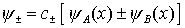
	Variationsansatz:   Die Wellenfunktion des Molekülelektrons wird als symmetrische (+) und antisymmetrische (-) Kombination von 1S Wellenfunktionen des H-Atoms angesetzt
	Energie der Zustände:
	S(R) = Überlappintegral =
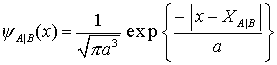
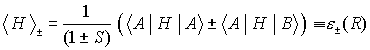
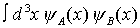
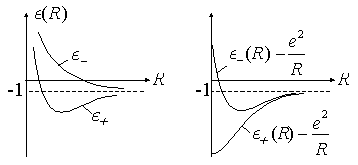
	Energie der Zustände         reine elektronische Energie 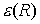enthält die Coulombabstoßung der Kerne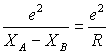
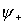	=>  ist bindend, d.h. 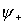ist zwischen den Kernen größer als  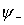=> größere Aufenthaltswahrscheinlichkeit des Elektrons zwischen den Kernen => niedrigere Energie
	Querverweise: Quantenmechanik:   Teilchen in einem Potentialtopf (qualitativ)   Das Wasserstoffmolekül (Wellenfunktionen der Elektronen bei festen Kernen)
	15.06.2001 - URL dieser Seite - Seite_ID: 5020002 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

3. Das Wasserstoffmolekül (Wellenfunktionen der Elektronen bei festen Kernen)

	Bildschirmexperimente zu diesem Thema:
	dim.modul Brechung und Totalreflexion [Beschreibung] [Download]
	Compton-Effekt [Beschreibung] [Download]
	Standfestigkeit [Beschreibung] [Download]
	Röntgenstrahlung [Beschreibung] [Download]
	dim.modul Federpendel [Beschreibung] [Download]
	Bildschirmexperimente und Beschreibungen: © dim.digitale medien  -  mehr Experimente...

	Literatur zu diesem Thema:
	Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop

sponsored Link: Meta-Preisvergleich


Kapitelübersicht
20. Moleküle

1. Born-Oppenheimer-Näherung

2. Das Wasserstoffmolekül mit nur einem Elektron

3. Das Wasserstoffmolekül (Wellenfunktionen der Elektronen bei festen Kernen)

4. Energie des Wasserstoffmoleküls

5. Kernwellenfuktion beim zweiatomigen Molekül

6. Van der Waals Kraft