Die Hauptgebiete 5. Quantenmechanik 4. Schrödinger-Gleichung  | 1. Schrödinger-Gleichung: |
 | Die Schrödinger-Gleichung für ein Teilchen in einem Potential folgt aus der Schrödinger-Gleichung für ein freies Teilchen in Analogie zur klassischen Hamilton-Funktion:  |
| Die Gültigkeit der Schrödinger-Gleichung wird vom Experiment bestätigt |
| Die Schrödinger-Gleichung ist eine Wellengleichung für die Wellenfunktionen, die Teilchen darstellen |
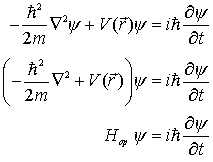
| Querverweise: Experimentalphysik 1-4: Bernoullische Gleichung Braggsche Gleichung Quantenmechanik: Von Neumann Gleichung Pauli Gleichung |
| 28.06.2000 - URL dieser Seite - Seite_ID: 5004001 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |
 | 2. Kontinuitätsgleichung |
 | Literatur zu diesem Thema: |
Unser Partner amazon.de liefert ab 20 Euro  - mehr Bücher im Buchshop |
 | Diskussionsbeiträge zu dieser Seite: (Neuer Beitrag) |
|
aus dem Physik-Forum:
|
|
| |
4. Schrödinger-Gleichung | 1. Schrödinger-Gleichung |
| 2. Kontinuitätsgleichung |
| 3. Bedingungen für die Wellenfunktion |
| 4. Impulsoperator und Hamiltonoperator (Ortsoperator) |
| 5. Schrödinger-Gleichung im Impulsraum |
| 6. Fouriertransformation der Wellenfunktion |
| 7. Eigenschaften der Wellenfunktion |
| 8. Erwartungswert eines Operators |