Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

22. Statistische Systembeschreibung

	4. Von Neumann Gleichung:
	Die Von-Neumann-Gleichung  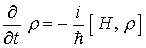beschreibt die Zeitentwicklung der Dichtematrix im Schrödingerbild (nicht zu verwechseln mit der Bewegungsgleichung für Operatoren im Heisenbergbild)
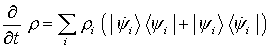
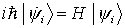
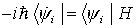
	Herleitung aus der Schrödingergleichung: mit  und  aus der Schrödingergleichung
	Die Von-Neumann-Gleichung ist das quantenmechanische Analogon zur Liouville-Gleichung der Mechanik
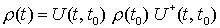	ergibt sich aus der Von-Neumann-Gleichung mit der formalen Lösung 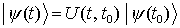der Schrödinger-Gleichung
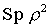	ist zeitunabhängig => Ein reiner/gemischter Zustand bleibt rein/gemischt
	Querverweise: Experimentalphysik 1-4:   Bernoullische Gleichung   Braggsche Gleichung Quantenmechanik:   Pauli Gleichung
	23.08.2001 - URL dieser Seite - Seite_ID: 5022004 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

5. Dichtematrix für Spin 1/2 Systeme

	Literatur zu diesem Thema:
	Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop

sponsored Link: Meta-Preisvergleich


Kapitelübersicht
22. Statistische Systembeschreibung

1. Dichtematrix für reine Gesamtheiten (statistischer Operator, Dichteoperator)

2. Dichtematrix für gemischte Gesamtheiten (in Diagonalform)

3. Dichtematrix in allgemeinster Form

4. Von Neumann Gleichung

5. Dichtematrix für Spin 1/2 Systeme

6. Polarisationsgrad von Spin 1/2 Systemen