Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

11. Sphärisch symmetrische Potentiale

	9. Normierung in sphärisch symmetrischen Potentialen:
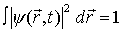	Die Normierung vereinfacht sich zu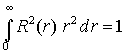 wegen der Normierung der Winkelfunktionen
	Die Kugelfunktionen sind normiert:
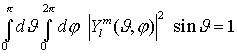
	Querverweise: Quantenmechanik:   Sphärisch symmetrischer Potentialtopf   Streuung am sphärisch symmetrischen Potential allgemein
	24.01.2001 - URL dieser Seite - Seite_ID: 5011009 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

10. Wahrscheinlichkeitsdichte - in kartesichen Koordinaten - in Kugelkoordinaten

	Literatur zu diesem Thema:
	Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop

sponsored Link: Meta-Preisvergleich


Kapitelübersicht
11. Sphärisch symmetrische Potentiale

1. Differentialbeziehungen in sphärischen Koordinaten

2. Drehimpulsoperator in sphärischen Koordinaten

3. Zeitunabhängige Schrödinger-Gleichung in sphärischen Koordinaten

4. Radiale Schrödinger-Gleichung

5. Legendre Polynome

6. Assozierte Legendre Funktionen

7. Kugelfunktionen

8. Gemeinsame Eingenfunktionen der z-Komponente und des Quadrates des Drehimpulsoperators

9. Normierung in sphärisch symmetrischen Potentialen

10. Wahrscheinlichkeitsdichte - in kartesichen Koordinaten - in Kugelkoordinaten

11. Leiteroperatoren