Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

12. Beispiele für sphärisch symmetrische Potentiale

	5. Sphärisch symmetrischer Potentialtopf:
	Potential:
	Radiale Schrödingergleichung:
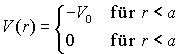
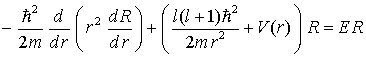
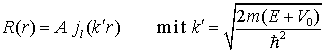
	für r < a ist die Lösung für E > 0: jl = sphärische Besselfunktion
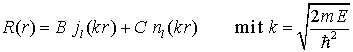
	für r > a ist die Lösung für E > 0: im Fall -V0 < E < 0 ist die Lösung für r > a:
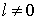	Wegen der Forderung R(0) = 0 (nur für ) gibt es nur ungerade Lösungen. Im eindimensionalen Fall gibt es gerade und ungerade gebundene Zustände
	Am Ursprung ist nur jl regulär
	Querverweise: Experimentalphysik 1-4:   Drehung mit symmetrischer / unsymmetrischer Massenverteilung zur Drehachse Quantenmechanik:   Teilchen in einem Potentialtopf (qualitativ)   Potentialtopf   Bestimmung der Energieeigenwerte beim eindimensionalen Potentialtopf   Normierung in sphärisch symmetrischen Potentialen   Streuung am sphärisch symmetrischen Potential allgemein
	27.01.2001 - URL dieser Seite - Seite_ID: 5012005 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

1. Schrödinger-Gleichung für ein 2-Teilchen-System

	Literatur zu diesem Thema:
	Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop

sponsored Link: Meta-Preisvergleich


Kapitelübersicht
12. Beispiele für sphärisch symmetrische Potentiale

1. Besselfunktionen

2. Bessel- Hankel und Neumannfunktionen

3. Freies Teilchen in Kugelkoordinaten

4. Entwicklung einer ebenen Welle nach sphärischen Wellen

5. Sphärisch symmetrischer Potentialtopf