
 | 
13. Variationsrechnung:
|
|
|
 | Die Variationsrechnung ist eine alternative Methode zur Berechnung von gestörten Energieeigenwerten (z.B. wenn eine geeignete Aufspaltung H = H0 + V nicht möglich ist)
|
|
|
 | Das Eigenwertproblem  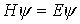 ist äquivalent zu dem Variationsproblem: Minimum von ( ist äquivalent zu dem Variationsproblem: Minimum von ( 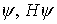 ) mit der Nebenbedingung ) mit der Nebenbedingung  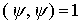 , Variation , Variation  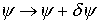
|
|
|
 | =>  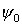 macht ( macht ( 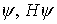 ) zum Minimum mit ) zum Minimum mit  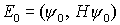 Grundzustandsenergie Grundzustandsenergie
|
|
|
 | Den nächsten Eigenwert findet man durch Minimalisierung von
( 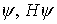 ) unter den Nebenbedingungen ) unter den Nebenbedingungen  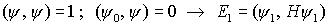
|
|
|
 | Höhere Zustände erhält man entsprechend
|
|
|
 | 08.03.2001 - URL dieser Seite - Seite_ID: 5015013
Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |



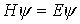 ist äquivalent zu dem Variationsproblem: Minimum von (
ist äquivalent zu dem Variationsproblem: Minimum von (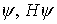 ) mit der Nebenbedingung
) mit der Nebenbedingung 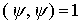 , Variation
, Variation 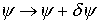

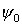 macht (
macht (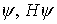 ) zum Minimum mit
) zum Minimum mit 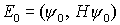 Grundzustandsenergie
Grundzustandsenergie 
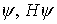 ) unter den Nebenbedingungen
) unter den Nebenbedingungen 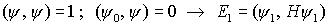


 - mehr Bücher im
- mehr Bücher im