
 | 
10. Bornsche Näherung in der Streutheorie:
|
|
|
 | Die Bornsche Näherung gilt, wenn die Energie des gestreuten Teilchens groß gegen das Streupotential  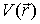 ist ist
|
|
|
 | In der Bornschen Näherung wird der Streuprozess als Überlagerung des Zustandes  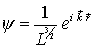 zum Zustand zum Zustand
 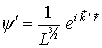 betrachtet (Das sind die Zustände eines freien Teilchens im Kasten L3) betrachtet (Das sind die Zustände eines freien Teilchens im Kasten L3)
|
|
|
 | Die Übergangsrate lässt sich mit Fermis goldener Regel berechnen
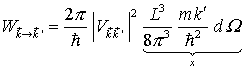
mit  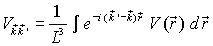
x = Dichte der Zustände mit Energie E und Streuwinkel  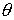
|
|
|
 | Der Wirkungsquerschnitt  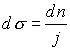 ist ist  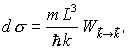
(mit der Stromdichte für die ebene Welle  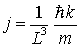 ) )
|
|
|
 | Der differentielle Wirkungsquerschnitt  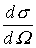 ist ist
 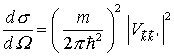 (wegen k = k') (wegen k = k')
|
|
|
 | Das Ergebnis erhält man auch durch Lösung der Schrödinger-Gleichung in erster Näherung Störungstheorie mit dem Streupotential V als Störung, die gewonnene Streuamplitude  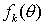 ist ist  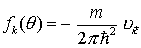 mit mit  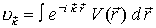
=> derselbe Wirkungsquerschnitt  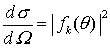
|
|
|
 | Die Bornsche Näherung ist ein Ergebnis der Störungstheorie 1. Ordnung
|
|
|
 | Querverweise:
Quantenmechanik: Vergleich mit der klassischen Streutheorie Beispiel: Bornsche Näherung im rotationssymmetrischen Potential
|
|
|
 | 19.02.2001 - URL dieser Seite - Seite_ID: 5014010
Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |


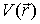 ist
ist 
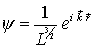 zum Zustand
zum Zustand 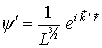 betrachtet (Das sind die Zustände eines freien Teilchens im Kasten L3)
betrachtet (Das sind die Zustände eines freien Teilchens im Kasten L3) 
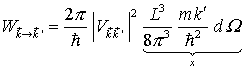
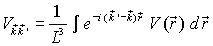
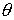

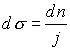 ist
ist 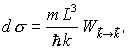
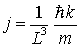 )
) 
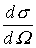 ist
ist 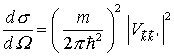 (wegen k = k')
(wegen k = k') 
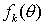 ist
ist 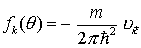 mit
mit 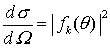



 - mehr Bücher im
- mehr Bücher im