Die Hauptgebiete 5. Quantenmechanik 17. Spin und Addition von Drehimpulsen  | 1. Matrixdarstellung der Drehimpulsoperatoren: |
 | Eigenwertgleichungen für den Drehimpulsoperator   :  |
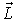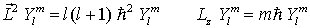
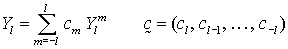| Eine Funktion Yl kann nach Ylm entwickelt werden:  2l + 1 Komponenten |
| Die Funktion Yl kann dargestellt werden durch den Vektor  |
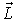| Die Komponenten von können als (2l + 1) 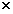(2l + 1) Matrizen dargestellt werden |
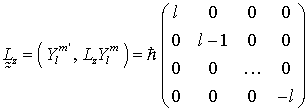
| Konstruktion der Matrizen: für Lz  Konstruktion von Lx Ly über L+ und L- |
| Für l = 1  |
| Für die Matrizen gelten dieselben Rechenregeln wie für die Operatoren z.B.  |
| Eigenzustände diagonalisieren die Operatormatrix |
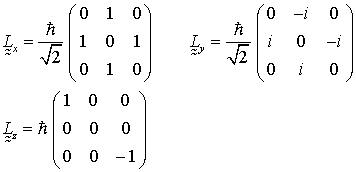
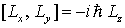
| Querverweise: Quantenmechanik: Matrixdarstellung eines Spinors (Dichtematrix) |
| 15.03.2001 - URL dieser Seite - Seite_ID: 5017001 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |
 | 2. Der Spin |
 | Literatur zu diesem Thema: |
Unser Partner amazon.de liefert ab 20 Euro  - mehr Bücher im Buchshop |
|
| |
17. Spin und Addition von Drehimpulsen | 1. Matrixdarstellung der Drehimpulsoperatoren |
| 2. Der Spin |
| 3. Eigenschaften der Pauli-Spinoren und Pauli-Matrizen |
| 4. Wellenfunktion eines Spin 1/2 Teilchens |
| 5. Stern-Gerlach-Experiment |
| 6. Zusammensetzung von Spins |
| 7. Zusammensetzung von Spin- und Bahndrehimpuls |
| 8. Gemeinsame Eigenfunktionen der z-Komponente und des Quadrates des Gesamtdrehimpulses |
| 9. Drehoperator des Spins |
| 10. Polarisationsvektor des Spinors |
| 11. Matrixdarstellung eines Spinors (Dichtematrix) |
| 12. Addition von Drehimpulsen: allgemeiner Fall |
| 13. Gemeinsame Eigenfunktionen der z-Komponente und des Quadrates des Gesamtdrehimpulses bei Addition von beliebigen Drehimpulsen |