Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

17. Spin und Addition von Drehimpulsen

	10. Polarisationsvektor des Spinors:
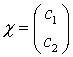	Zu einem beliebigen Spinor  kann man den Polarisationsvektor  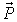konstruieren: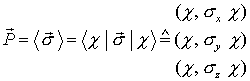
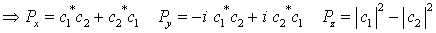
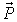	ist ein Einheitsvektor und gibt die Richtung des Spinors an
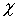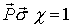
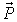	ist Eigenvektor von bei Eigenwert = 1:
	kann angegeben werden durch  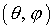 ( 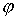in x-y Ebene):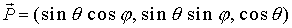
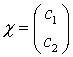	Ein beliebiger Spinor  geht aus  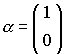(in z-Richtung) hervor, durch Drehung um  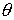um die Achse 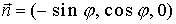in der x-y Ebene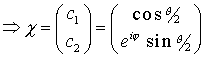
	Der Spinor ist bis auf einen Phasenfaktor eindeutig bestimmt  durch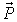:  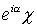hat den gleichen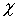  Vektor wie
	Querverweise: Quantenmechanik:   Matrixdarstellung eines Spinors (Dichtematrix)
	28.03.2001 - URL dieser Seite - Seite_ID: 5017010 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

11. Matrixdarstellung eines Spinors (Dichtematrix)

	Literatur zu diesem Thema:
	Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop

sponsored Link: Meta-Preisvergleich


Kapitelübersicht
17. Spin und Addition von Drehimpulsen

1. Matrixdarstellung der Drehimpulsoperatoren

2. Der Spin

3. Eigenschaften der Pauli-Spinoren und Pauli-Matrizen

4. Wellenfunktion eines Spin 1/2 Teilchens

5. Stern-Gerlach-Experiment

6. Zusammensetzung von Spins

7. Zusammensetzung von Spin- und Bahndrehimpuls

8. Gemeinsame Eigenfunktionen der z-Komponente und des Quadrates des Gesamtdrehimpulses

9. Drehoperator des Spins

10. Polarisationsvektor des Spinors

11. Matrixdarstellung eines Spinors (Dichtematrix)

12. Addition von Drehimpulsen: allgemeiner Fall

13. Gemeinsame Eigenfunktionen der z-Komponente und des Quadrates des Gesamtdrehimpulses bei Addition von beliebigen Drehimpulsen