Energieeigenwerte des Wasserstoffatoms - Physikon - lexikon lernportal studium schule homepage hausaufgabe buch referat facharbeit formelsammlung hausaufgaben

Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...

Javascript ist nicht aktiv!
Physikon ist nur voll funktionsfähig, wenn Sie die Javascript-Funktion in den Einstellungen Ihres Internetbrowsers aktivieren.

Die Hauptgebiete

5. Quantenmechanik

13. Wasserstoff Atom

	8. Energieeigenwerte des Wasserstoffatoms:


	Die Energieeigenwerte des Wasserstoffs ergeben sich aus der Abbruchbedingung der Potenzreihe beim Lösungsansatz für die radiale Schrödinger-Gleichung


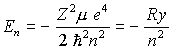	(CGS Ladungseinheit: 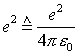) n = N + l + 1; n = 1, 2, 3, ...


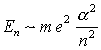
	Die Energieniveaus sind n²-fach entartet, d.h. es gibt n² verschiedene Wellenfunktionen mit dem gleichen Energieeigenwert. Entartungsgrad =


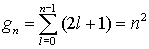
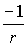	Die Unabhängigkeit der Energie von der Quantenzahl m folgt aus der Radialsymmetrie des Potentials (m kommt nicht in der Radialgleichung vor)


	Die Unabhängigkeit von der Energie von l ist eine spezielle Eigenschaft des Potentials, kann begründet werden mit der Existenz einer speziellen Erhaltungsgröße: Lenzscher Vektor


	Querverweise: Quantenmechanik: Energieeigenwerte des harmonischen Oszillators Bestimmung der Energieeigenwerte beim eindimensionalen Potentialtopf Normierte Wellenfunktionen des Wasserstoffatoms Radiale Wellenfunktionen des Wasserstoffatoms Quantenzahlen des Wasserstoffatoms Dirac-Gleichung des Wasserstoffatoms


	05.02.2001 - URL dieser Seite - Seite_ID: 5013008 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema