
3. Energieeigenwerte des harmonischen Oszillators:

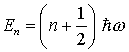 n = 0, 1, 2, ...
n = 0, 1, 2, ... 




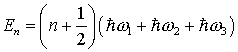 , weil das Problem separiert:
, weil das Problem separiert: 
Experimentalphysik 1-4: Energie des harmonischen Oszillators
Quantenmechanik: Schrödinger-Gleichung des harmonischen Oszillators Lösung der Schrödinger-Gleichung des harmonischen Oszillators Eigenfunktionen des harmonischen Oszillators Vergleich der klassischen und quantenmechanischen Behandlung des harmonischen Oszillators Algebraische Methode zur Bestimmung der Wellenfunktion des harmonischen Oszillators (mit Auf- und Absteigeoperatoren) Zustandssumme des harmonischen Oszillators Bestimmung der Energieeigenwerte beim eindimensionalen Potentialtopf Energieeigenwerte des Wasserstoffatoms
Schulphysik: Gesetze der harmonischen Schwingung Energie des harmonischen Oszillators Überlagerung von zwei harmonischen Schwingungen
Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

 - mehr Bücher im
- mehr Bücher im