Berechnung der zeitunabhängigen Schrödinger-Gleichung aus der zeitabhängigen - Physikon - lexikon lernportal studium schule homepage hausaufgabe buch referat facharbeit formelsammlung hausaufgaben

Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...

Javascript ist nicht aktiv!
Physikon ist nur voll funktionsfähig, wenn Sie die Javascript-Funktion in den Einstellungen Ihres Internetbrowsers aktivieren.

Die Hauptgebiete

5. Quantenmechanik

5. Zeitunabhängige Schrödinger-Gleichung

	2. Berechnung der zeitunabhängigen Schrödinger-Gleichung aus der zeitabhängigen:


	Zeitabhängige Schrödinger-Gleichung:


	Seperationsansatz:


	einsetzen:


	Division durch


	Links steht eine reine Funktion der Zeit, rechts eine reine Funktion des Ortes, deshalb müssen die linke und die rechte Seite konstant sein, damit die Gleichung für alle x und t erfüllt ist. Die Konstante ist E


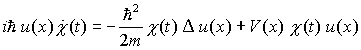
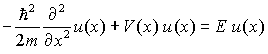
	=> für den räumlichen Anteil gilt die Gleichung Weil die linke Seite die Summe von kinetischer und potentieller Energie darstellt, ist E die Gesamtenergie


	=> für den zeitlichen Anteil gilt die Gleichung


	Querverweise: Experimentalphysik 1-4: Bernoullische Gleichung Berechnung der Entropie Braggsche Gleichung Quantenmechanik: Lösungen der zeitunabhängigen Schrödinger-Gleichung Lösung der zeitabhängigen Schrödinger-Gleichung - Entwicklung nach stationären Lösungen Qualitative Lösungen der zeitunabhängigen Schrödinger-Gleichung am Potentialberg Berechnung von stationären Lösungen mit der WKB-Methode Berechnung der Transmissionswahrscheinlichkeit mit der WKB-Methode Von Neumann Gleichung Pauli Gleichung Schulphysik: Berechnung von Trägheitsmomenten


	23.07.2000 - URL dieser Seite - Seite_ID: 5005002 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema