Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

7. Eindimensionale Potentiale

	7. Wasserstoffatom eindimensional:
	Gesucht werden gebundene Zustände des Elektrons im Potential
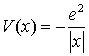
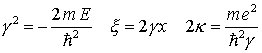	Mit den Größen erhält man aus der Schrödinger-Gleichung die Differentialgleichung für die Funktion :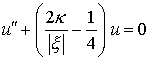
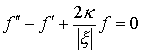
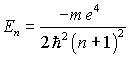
	Mit dem Ansatz ergibt sich folgende Differentialgleichung:
	Einsetzen des Reihenansatzes liefert eine Rekursionsbeziehung für die an
	Die Energieeigenwerte ergeben sich aus der Abbruchbedingung der Reihe
	Die Funktion ist ein Polynom
	Die Energieeigenwerte im eindimensionalen entsprechen dem dreidimensionalen Fall. Die Eigenfunktionen im eindimensionalen Fall sind vom dreidimensionalen Fall verschieden
	Querverweise: Quantenmechanik:   Wasserstoffatom - radiale Schrödinger-Gleichung   Wasserstoffatom im Magnetfeld   Alle Aufspaltungen am Beispiel n=2 im Wasserstoffatom
	07.10.2000 - URL dieser Seite - Seite_ID: 5007007 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

8. Potentialtopf

	Literatur zu diesem Thema:
	Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop

sponsored Link: Meta-Preisvergleich


Kapitelübersicht
7. Eindimensionale Potentiale

1. Teilchen im Potentialkasten

2. Entwicklung einer Funktion nach Eigenfunktionen des Potentialkastens

3. Transmissions- und Reflexionskoeffizient

4. Potentialstufe - für E<Stufenhöhe

5. Potentialstufe - für E>Stufenhöhe

6. Potentialbarriere

7. Wasserstoffatom eindimensional

8. Potentialtopf

9. Bestimmung der Energieeigenwerte beim eindimensionalen Potentialtopf

10. Bloch-Theorem

11. Kronig Penny Modell

12. Graphische Bestimmung der Bandstruktur beim Kronig Penny Modell

13. WKB-Näherung

14. Berechnung von stationären Lösungen mit der WKB-Methode

15. Berechnung der Transmissionswahrscheinlichkeit mit der WKB-Methode