Störungstheorie - Physikon - lexikon lernportal studium schule homepage hausaufgabe buch referat facharbeit formelsammlung hausaufgaben

Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...

Javascript ist nicht aktiv!
Physikon ist nur voll funktionsfähig, wenn Sie die Javascript-Funktion in den Einstellungen Ihres Internetbrowsers aktivieren.

Die Hauptgebiete

5. Quantenmechanik

15. Störungstheorie

	1. Störungstheorie:


	Die Störungstheorie ist ein Verfahren um Eigenwerte und Eigenfunktionen für solche Potentiale zu finden, deren Schrödingergleichung nicht analytisch lösbar ist


	Voraussetzung für die Störungstheorie ist ein gelöstes Problem mit bekanntem vollständigem Satz von Eigenfunktionen des Hamiltonoperators H₀:


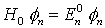
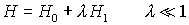	Der Hamiltonoperator des mit der Störungstheorie zu lösenden Problems H darf sich nur wenig von H₀ unterscheiden: H₁ = Störung d.h. die Energieeigenwerte von H sind nur wenig von denen von H₀ verschieden


	Gelöst werden muß


	Die Störungstheorie kann nicht angewendet werden wenn H₁ die physikalische Situation verändert, obwohl H₁ klein ist (z.B. H₁ macht aus einem anziehenden Potential ein abstoßendes)


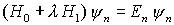
	Querverweise: Quantenmechanik: Zeitunabhängige Störungstheorie 1. Ordnung Zeitunabhängige Störungstheorie 1. Ordnung - Wellenfunktion Zeitunabhängige Störungstheorie 2. Ordnung Entartete Störungstheorie (1. Ordnung Energieverschiebung) Entartete Störungstheorie bei zweifacher Entartung Prinzip der entarteten Störungstheorie Zeitabhängige Störungstheorie normaler Zeemanneffekt mit Störungstheorie


	21.02.2001 - URL dieser Seite - Seite_ID: 5015001 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema