Zeitunabhängige Störungstheorie 1. Ordnung - Physikon - lexikon lernportal studium schule homepage hausaufgabe buch referat facharbeit formelsammlung hausaufgaben

Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...

Javascript ist nicht aktiv!
Physikon ist nur voll funktionsfähig, wenn Sie die Javascript-Funktion in den Einstellungen Ihres Internetbrowsers aktivieren.

Die Hauptgebiete

5. Quantenmechanik

15. Störungstheorie

	2. Zeitunabhängige Störungstheorie 1. Ordnung:


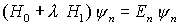	Zu lösen ist bekannt ist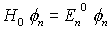


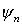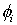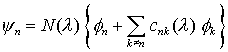
	Durch Entwicklung der Funktionen nach dem vollständigen Satz : und Einsetzen in die Schrödinger-Gleichung mit 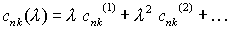und 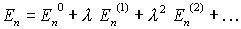ergibt sich wegen der Forderung 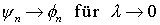mit Koeffizientenvergleich der Potenzen von :


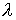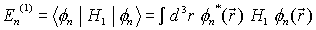
	Die Energieverschiebung des Zustandes E_n⁰ um E_n⁽¹⁾ ist in 1. Näherung der Erwartungswert des Störpotentials


	Die Entwicklungskoeffizienten für die Entwicklung von 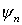nach den 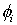sind in 1. Näherung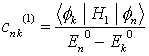


	Die Störung ist wesentlich wenn H₁ dort groß ist, wo auch 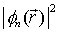groß ist


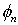	Die Energieverschiebung erster Ordnung E_n⁽¹⁾ verschwindet z.B. wenn gerade, H₁ ungerade ist


	Querverweise: Experimentalphysik 1-4: Zeitunabhängige Schrödingergleichung Quantenmechanik: Zeitunabhängige Schrödinger-Gleichung für ein freies Teilchen Zeitunabhängige Schrödinger-Gleichung Zeitunabhängige Schrödinger-Gleichung in sphärischen Koordinaten Störungstheorie Zeitunabhängige Störungstheorie 1. Ordnung - Wellenfunktion Zeitunabhängige Störungstheorie 2. Ordnung Entartete Störungstheorie (1. Ordnung Energieverschiebung) Entartete Störungstheorie bei zweifacher Entartung Prinzip der entarteten Störungstheorie Zeitabhängige Störungstheorie normaler Zeemanneffekt mit Störungstheorie


	22.02.2001 - URL dieser Seite - Seite_ID: 5015002 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema