normaler Zeemanneffekt mit Störungstheorie - Physikon - lexikon lernportal studium schule homepage hausaufgabe buch referat facharbeit formelsammlung hausaufgaben

Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...

Javascript ist nicht aktiv!
Physikon ist nur voll funktionsfähig, wenn Sie die Javascript-Funktion in den Einstellungen Ihres Internetbrowsers aktivieren.

Die Hauptgebiete

5. Quantenmechanik

18. Wasserstoff Atom II

	3. normaler Zeemanneffekt mit Störungstheorie:


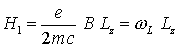
	Der Störoperator für schwache Magnetfelder in z-Richtung ist (folgt aus den elektromagnetischen Potentialen, Schrödingergleichung des Elektrons im elektromagnetischen Feld)


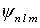	Weil die ungestörten Eigenfunktionen auch Eigenfunktionen von H₁ sind, ( 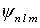sind Eigenfunktionen von L₂ und L_z: 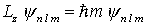) sind die Matrixelemente:


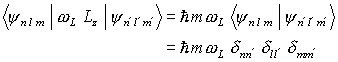
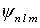	=> Die Störung koppelt nur Zustände mit gleichen n l m


	Weil die Zustände mit gleichem l entartet sind, muß die entartete Störungstheorie benutzt werden, die Störung ist hier diagonal, die Energieverschiebungen 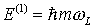sind die Diagonalelemente der Matrix h_ij


	Ein l Niveau spaltet in 2l + 1 Niveaus auf, weil , für den m Wert ist die Energieverschiebung


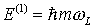
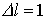	Aus einer Spektrallinie mit werden wegen der Auswahlregeln 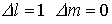und wegen der äquidistanten Aufspaltung nur drei Linien


	Querverweise: Quantenmechanik: Störungstheorie Zeitunabhängige Störungstheorie 1. Ordnung Zeitunabhängige Störungstheorie 1. Ordnung - Wellenfunktion Zeitunabhängige Störungstheorie 2. Ordnung Entartete Störungstheorie (1. Ordnung Energieverschiebung) Entartete Störungstheorie bei zweifacher Entartung Prinzip der entarteten Störungstheorie Zeitabhängige Störungstheorie


	11.04.2001 - URL dieser Seite - Seite_ID: 5018003 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema