Die Hauptgebiete 5. Quantenmechanik 8. Operatorenrechnung  | 7. Hermitezität von Operatoren: |
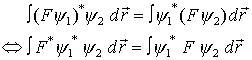
 | Definition: Ein linearer Operator ist hermitesch wenn gilt  für quadratintegrable Funktionen 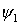  und  |
| => Der Erwartungswert eines hermiteschen Operators ist reell |
| Hermitesche Operatoren sind selbstadjungiert |
| Der Einheitsoperator I und alle Operatoren  sind hermitesch |
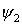
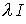| Ein beliebiger Operator kann als Summe eines hermiteschen und eines anti-hermiteschen Operators dargestellt werden:  anti-hermitesch |
| Querverweise: Quantenmechanik: Operatoren Linearität von Operatoren Anti-Hermitezität von Operatoren Eigenschaften von hermiteschen Operatoren Eigenschaften von adjungierten Operatoren Funktionen von Operatoren Einige Identitäten für Operatoren Eigenfunktionen und Eigenwerte von Operatoren |
| 29.10.2000 - URL dieser Seite - Seite_ID: 5008007 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema |
 | 8. Skalarprodukt von Funktionen |
 | Literatur zu diesem Thema: |
Unser Partner amazon.de liefert ab 20 Euro  - mehr Bücher im Buchshop |
|
| |
8. Operatorenrechnung | 1. Dirac'sche Notation |
| 2. Hilbertraum |
| 3. Basisunabhängige Darstellung der Wellenfunktion |
| 4. Orts- und Impulseingenfunktionen |
| 5. Operatoren |
| 6. Linearität von Operatoren |
| 7. Hermitezität von Operatoren |
| 8. Skalarprodukt von Funktionen |
| 9. Adjungierter Operator |
| 10. Anti-Hermitezität von Operatoren |
| 11. Eigenschaften von hermiteschen Operatoren |
| 12. Eigenschaften von adjungierten Operatoren |
| 13. Kommutator |
| 14. Funktionen von Operatoren |
| 15. Einige Identitäten für Operatoren |
| 16. Translationsoperator |
| 17. Paritätsoperator |
| 18. Zeitentwicklung von Erwartungswerten |
| 19. Heisenbergbild / Schrödingerbild |
| 20. Permutationsoperator |
| 21. Projektionsoperatoren |