Interaktives Physik-Lexikon und Lernsystem für Schüler und Studenten mit kompakten Erklärungen zur Physik, Bildschirmexperimenten, Physik-Aufgaben, Physik-Applets, Foren, Physik-Links, Suchfunktionen, Buchempfehlungen, News, Lernfunktion für Prüfungen ...
Die Hauptgebiete

5. Quantenmechanik

22. Statistische Systembeschreibung

	1. Dichtematrix für reine Gesamtheiten (statistischer Operator, Dichteoperator):
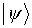	Betrachtet wird ein Ensemble von Systemen, die alle in demselben Zustand sind (reine Gesamtheit)
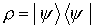
	Definition Dichtematrix  Für reine Gesamtheiten ist 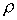 ein Projektionsoperator
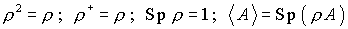
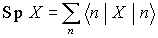
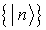	beliebiges vollständiges Orthonormalsystem
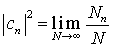
	Für ein Ensemble aus N Systemen gilt  Nn ist die Anzahl von Systemen (verändert sich mit N) bei denen sich bei Messung von A der Eigenwert an ergibt. 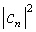ist die Wahrscheinlichkeit für ein System bei Messung von A den Eigenwert an zu finden
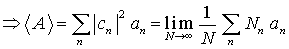
	Querverweise: Quantenmechanik:   Adjungierter Operator   Dichtematrix für gemischte Gesamtheiten (in Diagonalform)   Dichtematrix in allgemeinster Form   Dichtematrix für Spin 1/2 Systeme
	14.08.2001 - URL dieser Seite - Seite_ID: 5022001 Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema

2. Dichtematrix für gemischte Gesamtheiten (in Diagonalform)

	Literatur zu diesem Thema:
	Unser Partner amazon.de liefert ab 20 Euro  -  mehr Bücher im Buchshop

sponsored Link: Meta-Preisvergleich


Kapitelübersicht
22. Statistische Systembeschreibung

1. Dichtematrix für reine Gesamtheiten (statistischer Operator, Dichteoperator)

2. Dichtematrix für gemischte Gesamtheiten (in Diagonalform)

3. Dichtematrix in allgemeinster Form

4. Von Neumann Gleichung

5. Dichtematrix für Spin 1/2 Systeme

6. Polarisationsgrad von Spin 1/2 Systemen