Die Hauptgebiete
2. Dichtematrix für gemischte Gesamtheiten (in Diagonalform):
Zustand
; 
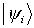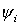sind orthonormiert 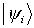zu finden ist 
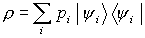
in Matrixdarstellung:
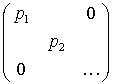
Die Dimension der Matrix ist die des Teilraumes vom Hilbertraum, der von den
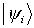aufgespannt wird. 
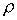ist nur in der Basis 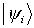diagonal 
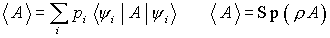
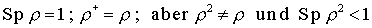
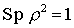(reine Gesamtheit) Bei gemischten Zuständen gilt
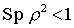(gemischte Gesamtheit) 
: 
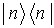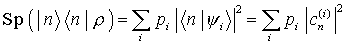
für kontinuierliche Spektren:
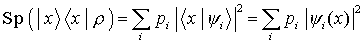
gibt die Wahrscheinlichkeit an, den Zustand
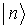bzw.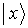 
als Meßergebnis zu erhalten 
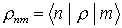
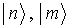sind Zustände einer Basis des von den 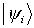aufgespannten Teilraumes des Hilbertraumes Experimentalphysik 1-4: Energiesatz für ideale Gase Gaußscher Satz für E- und D-Felder Fourier-Analyse für periodische Funktionen Fourier-Analyse für nicht periodische Funktionen Wellengleichung für elektromagnetische Wellen
Quantenmechanik: Schrödinger-Gleichung für ein freies Teilchen Zeitunabhängige Schrödinger-Gleichung für ein freies Teilchen Allgemeine Lösung der Schrödinger-Gleichung für ein freies Teilchen Bedingungen für die Wellenfunktion Qualitatives Verhalten der Lösung der Schrödinger-Gleichung für die Potentialmulde Potentialstufe - für E<Stufenhöhe Potentialstufe - für E>Stufenhöhe Einige Identitäten für Operatoren Schrödinger-Gleichung für ein 2-Teilchen-System Herleitung des Hamiltonoperators für geladene Teilchen im Magnetfeld Starkeffekt für den Grundzustand Starkeffekt für die Zustände mit n=2 Pauli Prinzip für wechselwirkende Teilchen Pauli Prinzip für nicht wechselwirkende Teilchen Hamilton-Operator für Materie, die mit dem Strahlungsfeld Wechselwirkt Auswahlregeln für elektrische Dipolübergänge Dichtematrix für reine Gesamtheiten (statistischer Operator, Dichteoperator) Dichtematrix in allgemeinster Form Dichtematrix für Spin 1/2 Systeme
Schulphysik: Beispiele für mechanische harmonische Schwingungen
Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema
- mehr Bücher im 