Die Hauptgebiete
9. Qualitatives Verhalten der Lösung der Schrödinger-Gleichung für die Potentialmulde:
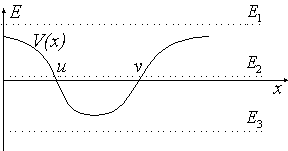
Schrödinger-Gleichung:
und 
für alle x dasselbe Vorzeichen => die Funktion ist konvex zur x-Achse => Wellenfunktionen sind nicht normierbar zwischen u und v konkav => oszillatorische Lösung, und außerhalb u v konvex => Divergenz oder Konvergenz, je nach 
an der Innenseite des Umkehrpunktes (ist stetig) => weil nur konvergente erlaubt sind ergeben sich nur bestimmte werte von E (gebundene Zustände), für die (u) und (v) einen erlaubten Wert haben 
bei u und v liegen Wendepunkte für alle x konkav => oszillatorische Lösungen, alle E-Werte möglich, Streuproblem: 
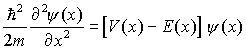
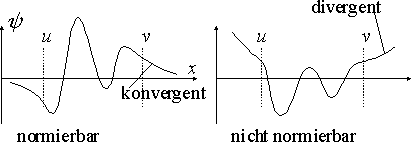
sind linear unabhängige Lösungen der Schrödinger-Gleichung, oszillierende stationäre Lösugen sind nicht normierbar, aber es lassen sich durch Linearkombination nichtstationäre normierbare Lösungen bilden: Wellenpakete Experimentalphysik 1-4: Bernoullische Gleichung Braggsche Gleichung Eigenschaften der Lösung der Schrödingergleichung
Quantenmechanik: Allgemeine Lösung der Schrödinger-Gleichung für ein freies Teilchen Lösung der zeitabhängigen Schrödinger-Gleichung - Entwicklung nach stationären Lösungen Lösung der Schrödinger-Gleichung des harmonischen Oszillators Von Neumann Gleichung Pauli Gleichung
Link zum Thema Eintragen - Beitrag zum Thema Schreiben - Persönliche Anmerkung - Diskussionsbeitrag zum Thema
- mehr Bücher im 